TEXTO Y DISCURSO

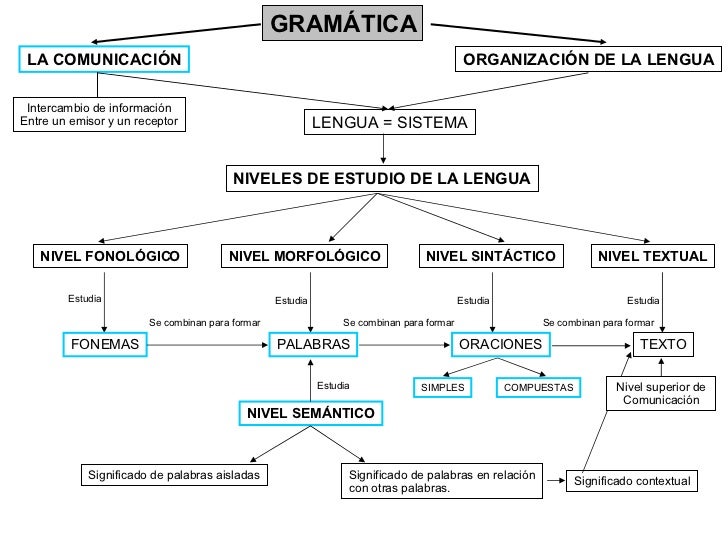
1.Esquema de gramática.

     
2.¿que es la lingüística textual?

Es una ciencia relativamente nueva, que se ampara en los conocimientos acumulados por la lingüística  cuyo objeto de estudio es el texto.

A partir de 1970, ocurrieron varios acontecimientos en la lingüística que cuestionaron el paradigma generativo-transformacional de Chomsky. El más importante es la presuposición de que la gramática de una lengua debe dar cuenta no sólo de las oraciones realizadas mediante las emisiones de hablantes nativos, sino también de las relaciones entre oraciones, o sea de los textos enteros subyacentes a estas emisiones.

2.¿que es un texto? ¿cuales son sus elementos?

Un texto es una composición de signos codificado en un sistema de escritura (como un alfabeto) que forma una unidad de sentido . Su tamaño puede ser variable.

También es texto una composición de caracteres imprimirles (con grafema) generados por un algoritmo de cifrado que, aunque no tienen sentido para cualquier persona, sí puede ser descifrado por su destinatario original.

Este texto o conjunto de signos extraídos de un discurso debe reunir condiciones de textualidad. Las principales son:

• Cohesión.
• Coherencia.
• Significado.
• Progresividad.
• Intencionalidad.
• Clausura o cierre.
• Adecuación.

2.1¿que es un discurso? ¿cuales son sus elementos?

según el uso corriente un discurso es un mensaje (verbal y oral) dirigido a un publico.
su principal función ha sido desde sus orígenes comunicar o exponer, pero con el objetivo principal de persuadir.
también podemos decir que un discurso es un acto de habla, y por tanto consta de los elementos de todo acto de habla.
El habla y el lenguaje son las herramientas que los seres humanos usan para comunicar o intercambiar pensamientos, ideas y emociones.

4. la teoría de las 6 lecturas apunta al análisis textual o al discursivo, sustente la respuesta.

la teoría de las seis lecturas apunta mas hacia la parte textual ya que esta teoría nos ayuda mas al modo de como escribir por medio de la interpretación.

5. Seleccione un articulo académico sobre la enseñanza de las matemáticas y aplique los niveles 3 y 4 de los seis niveles de lectura.

                                         Claves para enseñar matemáticas.

1. Dos pilares fundamentales de la enseñanza de las matemáticas son:

• El conocimiento de la materia: aquella anécdota del maestro que decía “expliqué el problema una vez y no lo entendieron, lo volví a explicar y tampoco lo entendieron, lo expliqué una tercera vez y entonces quien lo entendió fui yo”, es bastante real,
• Una buena didáctica: hay maestros, y muchos licenciados, que saben matemáticas pero a los que les falta pedagogía, saber explicar. No dominan la didáctica, que es la interrelación entre el dominio del propio saber, del contenido, y la capacitación de explicarlo a otros, de modo que esos otros hagan “su propio descubrimiento del concepto”.

2. El objetivo de la didáctica, en general, no es enseñar a los alumnos sino conseguir que los alumnos aprendan.

3. Enseñar no garantiza el aprendizaje.

4. La base de toda buena didáctica que ayuda a aprender es partir de la propia experiencia del alumno e introducir un interrogante. La experimentación es la base que nos conduce hacia el pensamiento lógico, que nos ayuda a estructurarlo. Pero es necesario, cuando experimentamos, introducir un interrogante relacionado con la experiencia y el entorno de vida del propio alumno. Con el interrogante provocamos un diálogo que nos lleva a relaciones y así implicamos el pensamiento lógico en la experiencia. Es básico que el niño sienta la necesidad de encontrar la respuesta a un problema, a una cuestión que no sabe resolver, que sea su propio interés lo que le lleve a querer descubrir cómo es tal cosa. Si no hay interrogante no hay evidencia del problema y no se produce descubrimiento. El verdadero aprendizaje es el propio descubrimiento.

5. Es más fácil decir “mirad, niños, para resolver tal cosa debéis hacer esto…”, pero eso no es educación, eso es adiestramiento. Dictar conocimientos no es construir aprendizaje.

6. Dicen que Pitágoras no resolvía nunca una raíz cuadrada, que las resoluciones de operaciones las hacían los esclavos. Pues en la escuela tenemos a los alumnos, mayoritariamente, haciendo este “trabajo de esclavos”, resolviendo mecánicamente operaciones cuyo sentido, además, no comprenden. Proceder mecánicamente, dejando de laso la comprensión, es abocar a los alumnos al fracaso escolar.

7. El alumno debe saber explicar lo que pasa, qué problema hay, cómo lo ha conseguido resolver…primero con la expresión verbal, después con la expresión escrita- dibujo o texto- y, finalmente, mediante el lenguaje matemático- números y signos- que ha de ser el final del proceso. Es una barbaridad iniciar el aprendizaje  de las matemáticas con el lenguaje numérico.

8. Los problemas son para hacer pensar, no para hacer calcular.

9. Los buenos problemas plantean situaciones nuevas, próximas a la realidad del alumno, e implican un reto que te hace pensar, imaginar…pueden admitir más de una solución.

Decodificación 2

puntuación:

"" encierra una idea
: hace una explicación
, separa ideas
... deja continuidad
. termina la idea

cromatizacion:

sin embargo, ademas, también.

pronominalizacion:

alumno - niño
maestro - profesor

inferencia proposicional:

La base para un buen conocimiento en matemáticas para un niño en la infancia es tratarles de enseñar por medio de la didáctica, cambiando así la parte monótona de los profesores antiguos.

Decodificación 3

macroproposiciones:

la experimentación es la base que nos conduce hacia el pensamiento lógico  que nos ayuda a estructurarlo, pero es necesario, cuando experimentamos, introducir un interrogante relacionado con la experiencia y el entorno de vida del propio alumno.